多群（3群以上）の解析方法（2） ノンパラメトリックの場合
1. ノンパラメトリックで３群以上
前回に引き続き３群以上の場合の比較方法です。t検定を用いることができない２群間比較のノンパラメトリック版で、Mann-WhitneyのU検定なるものがありましたが、３群以上の比較にもノンパラメトリック版がございます。その名もKruskal-Wallis検定と申しまして、例によって人名です。William H. Kruskal（ウィリアム・H・クラスカル）とW. Allen Wallis（W. アレン・ウォリス）により、1952年に提唱されました。歴史としてはMann-WhitneyのU検定が提唱されたのが1947年ですので、その５年後ということになりますか…。少し復習しますと、分散分析の帰無仮説は「比較している全ての群間に差は無い（=全ての群の平均値は一律である）」でした１）。Kruskal-Wallis検定もノンパラメトリック検定ですので、検定にはもちろん順位を用いるわけですが、帰無仮説、対立仮説はそれぞれ以下のようになります。
（=比較しているすべての群の理論上の順位和が理論値と等しい）
H₁（対立仮説）: 少なくとも1つの母集団の分布が、他の母集団の分布と異なる。
（=少なくとも1つ群の理論上の順位和が異なる）
これだけでは少々わかりにくいということで、例題で考えてみましょう。
2. Kruskal-Wallis検定の理論
では、例題で考えてみましょう。下記表１は前回同様、BMIと収縮期血圧の関係ですが、やはりBMIが大きいと血圧も高いのでしょうか？まずは、14のデータに対し、小さい方から順位を付与していきましょう。
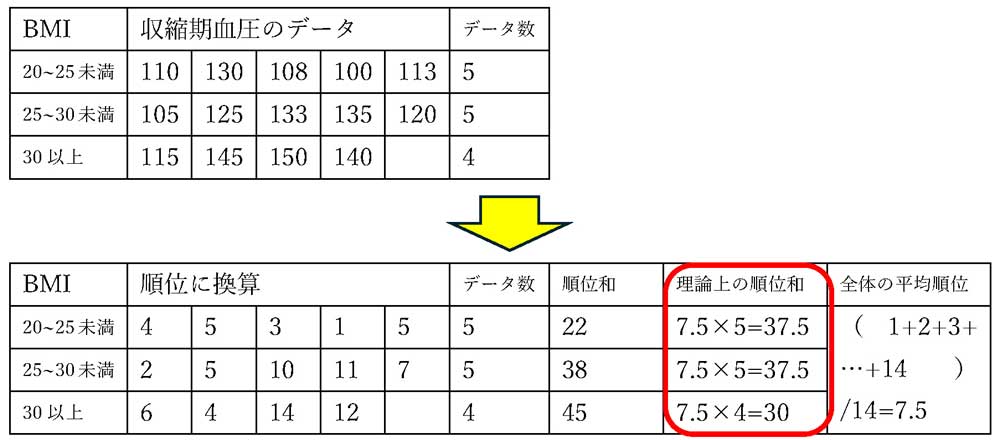
次に各群の順位の輪を求めてみます。BMIが小さい群から、22，38，45となりました。BMIが小さい群の方が順位和がより小さく、特にBMI30以上の群では、45と最も大きいようです。理論上の順位和は、1から14までの合計値の平均は7.5ですので、5人の群は7.5×5で37.5、4人の群は7.5×４で30になります。こうしてみますと、BMI30以上の群は、人数が少ないにも関わらず、順位和は最も大きくなりました。これは何かありそうですねということで理論式にはめてみましょう。
nは全体の症例数、niは各群の症例数、Riは順位和
H=12/14（14+1）×{（22）2/5+（38）2/5+（45）2/4}-
3（14+1）=5.96
α=0.05のときHα=5.666<Hとなるので、各群間で差があるといえる。
ところで上記の5.666とは？これは、このパターンの時のKruskal-Wallisが有意になる値であり、症例数の組み合わせによって値は異なります。今回の事例では４例と5例、５例の14例になりますので、下記はn1=4（最も小さい症例数が４の場合）のKruskal-Wallis統計量の表になります。n2=5,n3=5の交差する場所にある値に注目願います。検定統計量Hが、この値を超えたときにp<0.05となり、有意と判断されます。正規分布で例えるのであれば1.96、すなわちｐ値がちょうど0.05になる値、すなわち有意水準点であるということです。
このような表が必要になることがあるのか…と言われれば、まずありません。
執筆者について
経歴 ※このプロフィールは掲載記事執筆時点での内容となります
コメント
/
/
/
コメント